
Определение и планирование трудоемкости ремонта полиграфического оборудования в АССО
Автоматизированная система сервисного обслуживания (АССО) полиграфического оборудования, основными задачами которой являются организация и контроль выполнения заявок типографий на устранение неисправностей или планово-предупредительного ремонта полиграфических машин, требует наличия информации о номенклатуре и характеристике деталей, устройств и других элементов оборудования, порядке и составе технологических операций ремонта узлов и механизмов, о трудоемкости ремонтных работ и т.п. Для большинства современных полиграфических машин эта информация известна и содержится в инструкциях по их эксплуатации или сервисному обслуживанию. Однако парк оборудования многих полиграфических предприятий состоит не только из нового оборудования, но и включает подержанное оборудование. Для последнего многие данные регламента ремонтных работ, в том числе трудоемкость ремонта, часто отсутствуют или их нельзя считать достоверными.

Для организации ремонтных работ, выбора сервисной службы, определения стоимости ремонта, времени возможного простоя оборудования, заключения договоров на ремонт необходимо знать трудоемкость или время выполнения того или иного вида ремонта для каждой модели полиграфического оборудования. АССО на основании постепенно накапливаемых данных о выполнении ремонтных работ на различных машинах, которые содержатся в отчетах о выполнении ремонта, может определить среднее время ремонта. Необходимые данные по затратам времени на ремонт могут быть получены методом хронометража. По своей сущности хронометраж является видом наблюдения (в нашем случае — за процессом ремонта оборудования), при котором изучаются основные технологические операции, выполняемые ремонтным рабочим, например снятие и установка креплений с деталей и узлов, снятие и установка деталей, регулировка узлов и механизмов и т.п., а также отдельные элементы подготовительно-заключительной работы или работы по обслуживанию рабочего места. К подготовительно-заключительным, то есть вспомогательным, операциям можно отнести подготовку инструмента, смазочных и обтирочных материалов, распаковку и подготовку детали к установке, складирование поврежденной детали и т.п.
Основное назначение хронометража — определение продолжительности основных и вспомогательных технологических операций (приемов и движений) для расчета норм и разработки нормативов времени; выявление и изучение передовых методов и приемов труда в целях передачи этих методов работы широкому кругу работников; проверка установленных норм выработки; выявление причин невыполнения норм отдельными работниками. Метод хронометража хорошо соответствует характеру процесса, так как позволяет разделить его на основные и вспомогательные операции и рассчитать затраты времени на каждую из них в отдельности в зависимости от особенностей оборудования, которое подвергается профилактическим или ремонтным работам.
Хронометраж предполагает подробное изучение наблюдаемого процесса, его анализ и разбиение на элементы, позволяет определить количество необходимых наблюдений. Полученные в результате хронометража данные могут свидетельствовать о рациональности выполнения технологических операций, выполняемых в процессе ремонта. При этом возможно сокращение затрат времени за счет устранения отдельных элементов операций, замены некоторых приемов более рациональными и менее утомительными.
На практике используют два вида хронометража: непрерывный и выборочный. В первом случае замеры длительности элементов операций проводят непрерывно от начала до конца операции, а при выборочном хронометраже проводят замеры отдельных элементов операций. При проведении непрерывного хронометража в хронокарте отмечается время начала хронометража, а затем фиксируется по текущему времени окончание каждого элемента операции.
Результаты измерений подвергаются обработке, которая начинается с определения продолжительности выполнения отдельных элементов операции. При проведении непрерывного хронометража она равна разности показаний текущего времени двух смежных замеров. Затем исключаются ошибочные или так называемые дефектные замеры, о которых сделаны отметки при наблюдении. Дефектным считается такой замер времени, в течение которого рабочий выполнил элемент технологической операции дефектно (уронил деталь или инструмент, отошел, отвлекся и т.п.). Количество дефектных замеров, отмеченных при хронометраже, не должно превышать 15% от общего количества замеров данного хроноряда. Если количество дефектных замеров превышает 15%, то такой хронометражный ряд считается бракованным и соответствующий элемент (прием) операции подлежит повторному наблюдению. Затем составляют хронометражные ряды длительности выполнения каждого элемента операции во всех замерах.
Качество результатов наблюдения характеризуется величиной колебаний цифровых значений хроноряда. Эти колебания зависят от особенностей выполняемой работы, характера участия в ней рабочего, продолжительности элементов операций, типа операции, квалификации наблюдателя и рабочего, задействованных при измерении приборов. В связи с тем что затраты времени на ремонт зависят от квалификации исполнителей и хронометражиста, точности средства измерения, состояния инструмента, качества обработки данных хронометража, условий эксплуатации и конструктивных особенностей полиграфической машины, дискретные значения оперативного времени являются случайными величинами. Поэтому для определения среднего времени ремонта необходимо пользоваться методами математической статистики при обработке данных, полученных путем хронометража. По результатам хронометража определяют основное и вспомогательное время, затрачиваемое j-м исполнителем на выполнение i-й операции при ремонте. Данные хронометража проверяют на устойчивость по известному в математической статистике коэффициенту устойчивости: Куст=Tmax/Tmin
где Tmax и Tmin — соответственно наибольшая и наименьшая продолжительность операции в хроноряде.
Хроноряд считается устойчивым, если Куст ≤ 2,5. При невыполнении этого условия крайние значения в хроноряде отбрасываются. Среднее значение затрат времени Тср на выполнение ремонтной операции определяется с учетом полученных значений замеров Тi ( i=1…n) и числом замеров n по известной формуле:
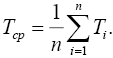
Хроноряд характеризуется также средним квадратическим отклонением:
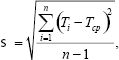
и коэффициентом вариации:
![]()
где n — количество измерений; Ti — результат i-го измерения.
Для каждого хроноряда технологической операции определяется относительная точность замеров:
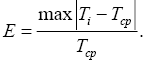
Абсолютная ошибка среднего арифметического значения трудоемкости подсчитывается по формуле:
![]()
Метрологической проверкой установлено, что предельная ошибка при определении трудоемкости технологических операций ремонта полиграфических машин не должна превышать 1,5%, а относительная ошибка обработки одного и того же хроноряда зависит от принятой точности подсчета и, как правило, не превышает 0,5%. Все остальные факторы, влияющие на точность получения результата, такие как точность приборов измерений, точность расчета в связи с их высокой точностью можно не учитывать.
Определение временн ых затрат на ремонтные работы с применением метода хронометража дает достаточно хорошие результаты, но сопряжено с очень большой протяженностью сбора статистических данных, по прошествии которого могут быть получены математически обоснованные достоверные данные. Это связано со случайным характером возникновения той или иной неисправности в конкретной модели полиграфической машины, возможностью проведения хронометража в момент ее ремонта и получения этой информации.
Для сокращения времени и экономии средств на сбор экспериментальных данных о трудоемкости ремонтных работ можно воспользоваться методами планирования эксперимента и многофакторного регрессионного анализа. Это позволит существенно сократить количество экспериментов, в данном случае — замеров времени продолжительности ремонта методом хронометража. При этом следует воспользоваться данными о трудоемкости ремонтов однотипного оборудования, при которых варьируются основные факторы, влияющие на длительность технологического процесса ремонта.
В отличие от традиционных форм выполнения экспериментов, методы математического планирования позволяют одновременно изучать влияние ряда факторов (многофакторный эксперимент) на исследуемый объект. Они основаны на математической теории эксперимента, которая определяет условия оптимального проведения исследования, в том числе и при неполном знании физической сущности явления. Для этого используют математические методы не только на стадии обработки результатов измерений, но также при подготовке и проведении опытов. Математические методы планирования эксперимента позволяют исследовать и оптимизировать сложные системы и процессы, обеспечивая высокую эффективность эксперимента и точность определения исследуемых факторов.
Для приближенного описания одного и того же явления можно предложить несколько моделей, оценка которых обычно производится по критерию Фишера. Поскольку степень полинома, адекватно описывающего процесс, предсказать невозможно, то сначала пытаются описать явление линейной моделью, а затем (если она неадекватна) повышают степень полинома, то есть проводят эксперимент поэтапно.
Одна из существенных концепций в теории планирования эксперимента — оптимальное использование факторного пространства. Она заключается в том, что состояние объекта в каждом опыте определяется по результату одновременного оптимального варьирования n факторов в n-мерном пространстве. Это позволяет добиться значительного увеличения точности расчета коэффициентов полученной модели и уменьшить трудоемкость эксперимента.
Наиболее широко применяются планы экстремального эксперимента, позволяющие описать исследуемый процесс и выполнить его оптимизацию. Они представляют собой систему опытов, содержащую возможные неповторяющиеся комбинации выбранных факторов при заданных уровнях их варьирования. Данный метод дает возможность одновременно изучать влияние многих факторов на исследуемый процесс и получить полином k-й степени (функцию отклика) для математического описания исследуемого процесса в некоторой локальной области факторного пространства, лежащего в окрестности выбранной точки с координатами
(z01, z02, ..., z0n) . Полученную функцию отклика можно также использовать для оптимизации процесса, то есть определять параметры, при которых явление или процесс будет протекать наиболее эффективно.
Экстремальный эксперимент основан на положении о том, что исследуемую непрерывную функцию
y – f(z1, z2, ..., zn),
имеющую все производные в заданной точке с координатами z01, z02, ..., z0n, можно разложить в ряд Тейлора:
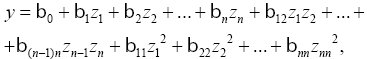
где β0 — значение функции отклика в начале координат z01, z02, ..., z0n;
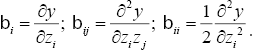 .
.
Ряд Тейлора аналогичен уравнению регрессии:
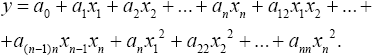
Здесь a0, ai, aij, aii— коэффициенты регрессии; xi — кодированная переменная, введенная в целях упрощения арифметических расчетов и равная
![]()
Следовательно, xi — относительное: максимальному значению zimax соответствует xi = +1, минимальному — zimin – xi = –1.
Коэффициенты регрессии вычисляются методами математической статистики и представляют собой приближенную оценку коэффициентов β0, βi, βii, ... ряда Тейлора. Следовательно, уравнение регрессии описывает исследуемый объект (процесс) только с определенной степенью точности.
Уравнение регрессии широко применяют для получения математической модели объектов исследования, хотя оно и не содержит необходимой информации о механизме явления и его физико-химических свойствах.
Планы оптимального эксперимента реализуются в такой последовательности:
1. Оценка информации и определение n факторов, наиболее существенных для исследуемого процесса.
2. Использование математической модели в виде линейной функции отклика.
3. Анализ выбранной модели.
4. Нахождение экстремума в области n-мерного факторного пространства путем использования полинома k-й степени.
5. Если модель неадекватна, то в качестве модели выбирают полиномы более высокого порядка.
Статистический анализ результатов экспериментов состоит из определения дисперсии воспроизводимости; определения оценок коэффициентов уравнения регрессии и проверки их значимости с использованием t-критерия Стьюдента; проверки гипотезы об адекватности модели с применением F-критерия Фишера.
На трудоемкость ремонта полиграфического оборудования может влиять целый ряд производственных, организационных, технологических и человеческих факторов, что серьезно усложняет выбор существенных из них для проведения экспериментальных исследований. Поэтому формирование списка факторов, необходимых для проведения исследования, целесообразно выполнять на основе мнений экспертов, при этом применяются различные специализированные экспертные процедуры, позволяющие добиться согласованности и компетенции мнений экспертов.
Поскольку на длительность выполнения различных технологических операций по ремонту полиграфического оборудования влияют различные факторы, формирование их списка целесообразно осуществлять в несколько этапов.
В нашем случае на первом этапе формирования списка факторов был проведен опрос экспертов для составления списка факторов, характеризующих сложность и трудоемкость ремонта. Всего было опрошено восемь человек: сотрудники ремонтных служб и технические руководители типографий. Мнения экспертов после опроса в первом туре были сведены в таблицы.
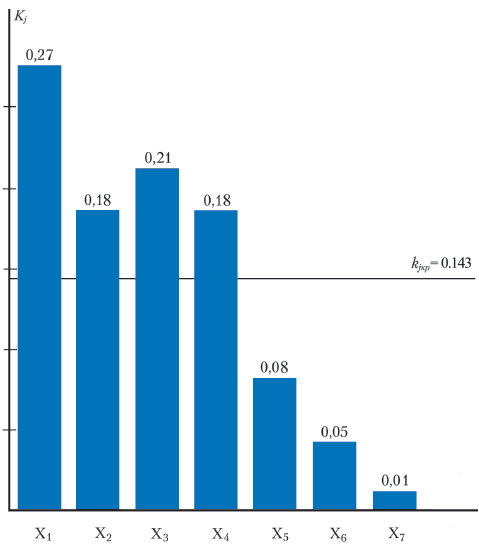
Результаты ранжирования параметров трудоемкости ремонта
После первого тура опроса экспертов был выявлен ряд факторов, которые, по мнению экспертов, влияют на длительность ремонта полиграфического оборудования. Каждый эксперт был ознакомлен со списками, которые подали другие эксперты, а затем был проведен второй тур, в ходе которого экспертам было предложено дополнить свои списки с учетом информации, полученной по результатам первого тура.
По результатам второго тура опроса экспертов новых факторов не появилось. Это говорит о том, что список полон, более того, некоторые эксперты отказались от ряда факторов и исключили их из поданных ими списков.
В результате в список факторов (параметров), характеризующих сложность и трудоемкость ремонта полиграфического оборудования с присвоением им кодов (X1 , …, X7 ), было включено семь факторов (табл. 1).
Таблица 1
Код |
Наименование фактора |
X1 |
Количество снимаемых деталей при ремонте |
X2 |
Общая масса снимаемых деталей |
X3 |
Количество снимаемых креплений |
X4 |
Количество регулировок |
X5 |
Масса снимаемой детали |
X6 |
Номенклатура стандартного инструмента |
X7 |
Номенклатура специального инструмента |
Третий этап опроса экспертов проходил в виде диалога. Для выбора наиболее существенных факторов была проведена процедура ранжирования факторов по степени значимости, для чего каждому фактору был присвоен порядковый номер — код фактора и ранги, значения которых присваивались в диапазоне от 0 до 10. Результаты сведены в табл. 2.
Таблица 2
Шифр эксперта |
Ранговые оценки |
Si |
Ti |
||||||
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
|||
1 |
1 |
3 |
2 |
4 |
5 |
6 |
7 |
28 |
– |
2 |
1 |
2,5 |
2,5 |
4 |
5 |
6 |
7 |
28 |
0,5 |
3 |
2 |
3,5 |
1 |
3,5 |
5 |
7 |
6 |
28 |
0,5 |
4 |
1,5 |
3,5 |
3,5 |
1,5 |
6 |
5 |
7 |
28 |
1 |
5 |
1 |
4 |
2 |
3 |
5 |
6 |
7 |
28 |
– |
6 |
1,5 |
1,5 |
3,5 |
3,5 |
6 |
5 |
7 |
28 |
1 |
7 |
1 |
3,5 |
3,5 |
2 |
5 |
6 |
7 |
28 |
0,5 |
8 |
1 |
3,5 |
2 |
3,5 |
5 |
6 |
7 |
28 |
0,5 |
Sj |
10 |
25 |
20 |
25 |
42 |
47 |
55 |
224 |
4 |
mn-S j |
46 |
31 |
36 |
31 |
14 |
9 |
1 |
|
|
Кj |
0,27 |
0,18 |
0,21 |
0,18 |
0,08 |
0,05 |
0,01 |
1,0 |
|
Кj0 |
0,32 |
0,22 |
0,25 |
0,22 |
|
|
|
1,0 |
|
Sj-S |
-22 |
-7 |
-12 |
-7 |
10 |
15 |
23 |
|
|
(Sj-S)2 |
484 |
49 |
144 |
49 |
100 |
225 |
529 |
1580 |
|
В указанной таблице: Si = const; Ti — оценка связей восьми одинаковых рангов; Sj — групповая оценка весомости j-го фактора.
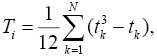
где N – общее число связей (групп одинаковых рангов), данных i-м экспертом (k = 1, N), tk — длина k-й связи.
Сумма рангов, присвоенных группой экспертов j-му фактору, определяется по формуле:
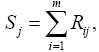
где Rij — ранговые оценки фактора, данные экспертами; m — число экспертов; Kj — коэффициент значимости:
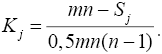
При выделении из n факторов n0 наиболее значимых факторов, для которых Kj ≥ Kjkp = 1/n (n = 7), то есть Kj ≥ 1/7 = 0,143, рассчитывались коэффициенты значимости Kj0:
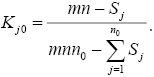
Результаты ранжирования графически представлены на диаграмме.
Для проверки согласованности суждений вычисляем коэффициент конкордации W:
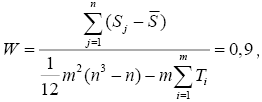
где S — средняя сумма рангов;
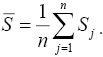 .
.
Проверка значимости коэффициента конкордации с помощью критерия Пирсона ![]() :
:
![]()
При этом ![]() табл(α,
табл(α, ![]() ) = 12,6, где α — уровень значимости (α = 0,05);
) = 12,6, где α — уровень значимости (α = 0,05); ![]() = n–1— число степеней свободы (
= n–1— число степеней свободы (![]() = 6).
= 6).
Поскольку ![]() >
> ![]() табл(α,
табл(α, ![]() ), то с вероятностью 95% можно утверждать, что суждения экспертов являются согласованными.
), то с вероятностью 95% можно утверждать, что суждения экспертов являются согласованными.
Соответственно действительно значимыми факторами, оказывающими влияние на длительность ремонта, являются:
- количество снимаемых деталей при ремонте;
- общая масса снимаемых деталей;
- количество снимаемых креплений;
- количество регулировок.
Данные параметры ремонта могут быть использованы для планирования эксперимента и построения многофакторной регрессионной модели для прогнозирования путем расчета трудоемкости ремонта.
Для прогнозирования АССО ориентировочного значения времени, которое может потребоваться на выполнение ремонтных работ, разработана линейная регрессивная модель зависимости ремонта от ряда факторов (параметров), характеризующих сложность ремонтных работ.
Проведенные экспертные оценки значимости предложенных параметров показали, что при определении результирующего фактора (времени ремонта) в регрессивной модели целесообразно учитывать только количество снимаемых деталей Nд, количество снимаемых креплений Nк, количество регулировок Nр, а также общую массу снимаемых деталей m.
Для одного типа полиграфического оборудования — листовых печатных офсетных машин среднего формата — было спланировано два варианта многофакторного эксперимента. Первый вариант для ремонта, в котором m ≤ 50 кг, а второй — для m > 50 кг. Для этих вариантов были составлены матрицы планирования эксперимента (табл. 3).
Таблица 3. Матрица планирования эксперимента
№№ п/п |
x0 |
Матрица планирования |
x1x2 |
x1x3 |
x2x3 |
x1x3x3 |
||
x1 |
x2 |
x3 |
||||||
1 |
+ |
– |
– |
– |
+ |
+ |
+ |
– |
2 |
+ |
+ |
– |
– |
– |
– |
+ |
+ |
3 |
+ |
– |
+ |
– |
– |
+ |
– |
+ |
4 |
+ |
+ |
+ |
– |
+ |
– |
– |
– |
5 |
+ |
– |
– |
+ |
+ |
– |
– |
+ |
6 |
+ |
+ |
– |
+ |
– |
+ |
– |
– |
7 |
+ |
– |
+ |
+ |
– |
– |
+ |
– |
8 |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
+ |
При планировании эксперимента и анализе результатов использовалась модель вида:
![]()
где y — время ремонта; x1 — количество снимаемых деталей при ремонте; x2 — количество снимаемых креплений; x3 — количество регулировок.
Планирование проводилось на двух уровнях, и данные об эксперименте вносились в матрицу планирования в кодированном виде. Данные вычислялись по соотношению:
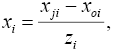
где xij и x0i — соответственно j-й и основной уровни i-го фактора; zi — интервал варьирования i-го фактора ![]() ;
; ![]() — верхний и нижний уровни i-го фактора.
— верхний и нижний уровни i-го фактора.
Кодированные значения факторов составили +1 и –1. Значения основного, верхнего и нижнего уровней факторов приведены в табл. 4 для модели при m ≤ 50 кг, в табл. 5 — для модели при m > 50 кг.
Таблица 4. Уровни воздействия факторов (при m ≤ 50 кг)
xi |
Факторы |
x0i |
xHi |
xBi |
zi |
x1 |
Количество снимаемых деталей Nд |
4 |
2 |
6 |
2 |
x2 |
Количество снимаемых креплений Nк |
16 |
8 |
24 |
8 |
x3 |
Количество регулировок Nр |
3 |
2 |
4 |
1 |
Таблица 5. Уровни воздействия факторов (при m > 50 кг)
xi |
Факторы |
x0i |
xHi |
xBi |
zi |
x1 |
Количество снимаемых деталей Nд |
3 |
2 |
4 |
1 |
x2 |
Количество снимаемых креплений Nк |
12 |
8 |
16 |
4 |
x3 |
Количество регулировок Nр |
3 |
2 |
4 |
1 |
В банке данных автоматизированной системы сервисного обслуживания, содержащем сведения о времени выполнения ремонтных работ, накопленные за последние два-три года, были подобраны значения этого времени. При этом использовались только данные о выполнении ремонтных работ, полученные в результате ремонта указанного типа машин и с соответствующими матрице планирования параметрами.
Для построения регрессионной модели трудоемкости ремонта листовых печатных машин при условии, что m ≤ 50 кг, было подобрано необходимое количество данных, которое в соответствии с матрицей планирования составило N = 2k∙m наблюдений, где k — количество исследуемых факторов (k = 3), m — количество опытов в каждой точке плана (m = 3), то есть N = 24 наблюдения.
В результате статической обработки наблюдений было получено уравнение регрессии вида:
![]() .
.
Подставив в найденное уравнение регрессии значения параметров (см. табл. 4) Nд (количество снимаемых деталей) Nк (количество снимаемых креплений) и Nр (количество регулировок) и перейдя от кодированных значений факторов к натуральным значениями:
![]() ,
,
после преобразования получим уравнение, являющееся регрессионной моделью трудоемкости ремонта Tр листовых офсетных печатных машин в зависимости от параметров сложности ремонта при условии, что общая масса снятых деталей при ремонте m ≤ 50 кг, и заменив упрогн. на Tр в виде:
![]()
Для построения регрессионной модели трудоемкости ремонта листовых печатных машин при условии, что m > 50 кг, в банке данных автоматизированной системы было подобрано 24 значения продолжительности времени ремонта. При этом кодированные значения факторов были занесены в табл. 5.
В результате статистической обработки наблюдений получено уравнение регрессии вида:
![]() .
.
Подставив в найденное уравнение вместо кодированных значений натуральные значения параметров (см. табл. 5) Nд (количество снимаемых деталей) Nк (количество снимаемых креплений) и Nр (количество регулировок):
![]() ,
,
после преобразования получим регрессионную модель трудоемкости ремонта Tр листовых офсетных печатных машин при условии, что общая масса снятых деталей при ремонте m > 50 кг, в виде:
![]() , мин,
, мин,
где N д, N к и N р — соответственно количество снимаемых деталей, креплений и регулировок.
Аналогичные регрессионные модели могут быть получены и для других типов полиграфических машин на основе данных, содержащихся и вновь поступающих в банк данных АССО. Эти модели могут быть использованы системой для расчета затрат времени на ремонт, знать которые необходимо для автоматизированной организации технического обслуживания.
