В лесах фрактальной графики. Часть 2

Дмитрий Шахов, фрилансер, г.Москва

В данной статье мы с вами поговорим о генераторах фракталов. Как известно, визуализация, или построение фрактального рисунка, осуществляется по какому-либо алгоритму или путем автоматической генерации изображений при помощи вычислений по конкретным формулам.

Дальнейшие изменения значений в алгоритмах или коэффициентах в формулах приводят к модификации этих изображений. Существуют генераторы фракталов, которые, в принципе, своим возникновением обязаны исследованиям фрактальной геометрии Бенуа Мандельброта, а также его совместным работам в области информатики с Ричардом Фоссом и Кеном Масгрейвом. В 1977 году Бенуа Мандельброт написал книгу «Фрактальная геометрия природы». В ней он подробно рассказал, как ручными математическими инструментами нарисовать сложный и красивый самоподобный узор.

Однако вычислительные инструментальные средства с автоматизированными вычислениями и выводом на печать позволили обойти бесконечные расчеты и операции с логарифмическими линейками вследствие очень быстрых итеративных операций. В 1980­е годы Кен Масгрейв трудился над методом реалистичных изображений ландшафтов с помощью математического аппарата фракталов. Во многом благодаря его работам и возникло так называемое алгоритмическое искусство. В дальнейшем на основе его алгоритмов генерации изображений была создана такая известная программа, как Bryce («Брайс»), предназначенная для 3D­моделирования, рендеринга и анимации и специализирующаяся на генерировании фрактальных пейзажей. Кроме того, в 1985 году журнал Scientific American представил алгоритм для вычисления множества Мандельброта для широкой аудитории. Таким образом, в 1980­е годы и были заложены первые кирпичики разросшегося сегодня направления в компьютерной графике.

В настоящее время существует достаточно большое количество программ для визуализации фракталов, проще говоря — фракталогенераторов. Но начнем мы, пожалуй, с одной из самых популярных и любимых фрактальщиками всего мира программ —Apophysis.

Рис. 1. Результаты работы редактора фрактальной графики Apophysis

Apophysis («Апофиз») (от греч. apofusiV — отросток) — редактор фрактальной графики (рис. 1) с открытым исходным кодом для визуализации в Microsoft Windows (также поддерживается Linux или Mac OS). Разработан Марком Таунсендом и переведен с языка С на язык программирования Delphi Скоттом Дрейвсом с добавлением графического пользовательского интерфейса. Очень распространенная в настоящее время среди цифровых художников программа Apophysis 7X является логическим продолжением более ранней версии программы Apophysis, от которой она отличается более многочисленными усовершенствованиями функций и пользовательского интерфейса, поддержкой большого количества встраиваемых плагинов и усовершенствованным кодом.

Следует отметить, что «Апофиз» визуализирует фракталы с помощью алгоритма, именуемого Fractal flames (дословно «фрактальное пламя» или «фрактальные искры»). Именно этот алгоритм был разработан Скоттом Дрэйвсом и, по сути, является частью метода «систем итерируемых функций».

Метод «систем итерируемых функций» (Iterated Functions System, IFS) появился в середине 1980­х годов как простое средство для получения фрактальных структур. IFS представляет собой систему функций из некоторого фиксированного класса функций, отображающих одно многомерное множество на другое. Наиболее простая IFS состоит из аффинных преобразований плоскости.

В 1988 году известные американские специалисты в теории динамических систем и эргодической теории Барнсли и Слоан предложили некоторые идеи, основанные на соображениях теории динамических систем, для сжатия и хранения графической информации и сформулировали их в виде метода фрактального сжатия информации. Происхождение названия связано с тем, что геометрические образы, возникающие в этом методе, обычно имеют фрактальную природу в смысле Мандельброта.

На основании своих идей Барнсли и Слоан создали алгоритм, который, по их утверждению, позволит сжимать информацию в 500­1000 раз. Вкратце метод можно описать следующим образом. Изображение кодируется несколькими простыми преобразованиями (в нашем случае аффинными), то есть коэффициентами этих преобразований (в нашем случае A, B, C, D, E и F).

Например, закодировав какое­то изображение двумя аффинными преобразованиями, мы однозначно определяем его с помощью 12 коэффициентов. Если теперь задаться какой­либо начальной точкой (например, X = 0, Y = 0) и запустить итерационный процесс, то после первой итерации мы получим две точки, после второй — четыре, после третьей — восемь и т.д. Через несколько десятков итераций совокупность полученных точек будет описывать закодированное изображение. Но проблема состоит в том, что очень трудно найти коэффициенты IFS, которые кодировали бы произвольное изображение.

Кроме аффинных, для построения IFS применяют и другие классы простых геометрических преобразований, которые задаются небольшим числом параметров. Например, проективные или квадратичные преобразования на плоскости.

Алгоритм Fractals flames отличается от IFS по следующим пунктам:

•    итерация нелинейных функций вместо аффинных преобразований;

•    отображение журнала плотности вместо линейной или бинарной;

•    окрашивание по структуре (то есть по пройденным рекурсивным путям) вместо монохромного окрашивания или окрашивания по плотности.

На основе этого же алгоритма работают и некоторые другие генераторы фракталов, например JWildFire — мощный редактор фрактальной графики. По функциональности его можно сравнить с Apophysis. Так же как и Apophysis, JWildFire работает с флеймами, но в отличие от «Апофиза», написанного на Delphi, он написан на языке Java.

Рис. 2. Примеры фракталов из классических множеств, синтезированных в программе FE

Другой известной программой является Fractal Explorer (рис. 2), которая позволяет создавать фракталы, основанные на классических множествах (множество Мандельброта, множество Жюлиа, множество Ньютона и их вариации), а также на некоторых других. Например, комплексные 4D­фракталы (фракталы, основанные на кватернионах), «странные» 3D­аттракторы, а также IFS­системы. Кроме того, в Fractal Explorer предусмотрено множество функций для создания различных эффектов и улучшения качества генерируемых изображений.

Рис. 3. Примеры изображения фрактальных множеств, синтезированных в программе UF

Следующая программа — Ultra Fractal — написана на Delphi и позволяет создавать изображения фрактальных множеств (рис. 3), а также выполнять их анимацию. Процесс построения изображений в ней определяется набором алгоритмов, описывающих разновидности визуализируемых фракталов, методы их раскраски и применяемые к ним трансформации. По принципу генерации программа практически не отличается от Fractal Explorer. Указанные алгоритмы представляются в виде текстовых файлов, написанных на специальном языке программирования, поддерживающем такие базовые конструкции, как массивы, функции, циклы и классы. Модульная архитектура написания алгоритмов позволяет пользователю создавать собственные.

Аналогично Adobe Photoshop, программа Ultra Fractal умеет работать с альфа­каналами, слоями и масками, что позволяет легко комбинировать различные фрагменты изображений.

Помимо вышеназванных программ существует довольно много генераторов, общей отличительной особенностью которых является создание 2D­ или псевдо­3D­изображений. Но есть и другие программы — фракталогенераторы, выполняющие визуализацию на основе трассировки лучей, а следовательно, создающие трехмерные изображения.

Рис. 4. Примеры изображений, синтезированных фракталогенератором Mandelbulb 3D

Одним из самых популярных среди «фрактальщиков» 3D­фракталогенератором является программа Mandelbulb 3D, которая представляет собой фрактальный рэй трейсер и позволяет работать с трехмерными фракталами (рис. 4). Множество настроек, включая настройки цвета, освещения, постобработки, глубины и т.д., позволит оптимально реализовать творческий замысел и обеспечит необходимую гибкость при работе. Программа поддерживает анимацию, является бесплатной и постоянно обновляемой. По сути, она работает на основе множества формул или алгоритмов, постоянно обновляемых разработчиками и пользователями и с трассировкой лучей. Mandelbulb — это трехмерный аналог множества Мандельброта, которое было впервые теоретически описано Пьером Фату в 1905 году и получено Бенуа Мандельбротом в 1975­м с помощью машинных устройств, недоступных П. Фату, и является двумерным. К концу 2007 года небольшой группой энтузиастов с форумов было принято решение о разработке алгоритмов и программного обеспечения для рендеринга 3D­фракталов на основе множества Мандельброта. Визуализация первых фракталов была неимоверно трудной из­за малого количества доступной в то время машинной памяти, а также отсутствия пользовательского интерфейса. После добавления интерфейса и многих других формул были разработаны Mandelbulb 3D и Mandelbulber, которые в настоящее время считаются одними из передовых в этой области программных средств.

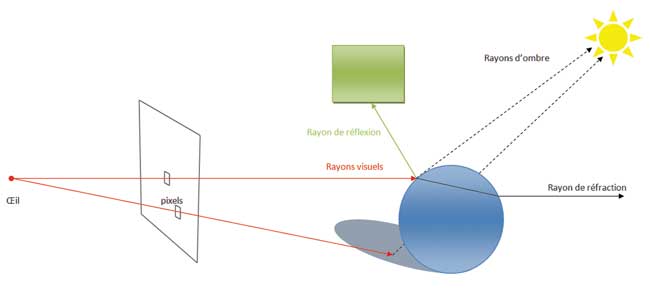
Рис. 5. На схеме показан процесс построения объекта путем трассировки и взаимоотношения лучей от наблюдателя и лучей освещения, отражения и рефракции (первичные и вторичные лучи)

Термин «рэй трейсер» переводится на русский язык как «трассировщик лучей», то есть данная программа при построении фрактальной сцены и для достижения фотографической реалистичности использует технологию трассировки лучей (рис. 5). Рассмотрим вкратце эту технологию. Основная идея трассировки лучей заключается в следующем: для каждого пиксела на дисплее движок рендеринга проводит прямой луч от глаза наблюдателя до элемента выводимой сцены. Первое пересечение используется для определения цвета пиксела как функции пересекаемой поверхности элемента. В дальнейшем необходимо определить освещение пиксела, что требует проведения вторичных лучей. В отличие от первичных лучей, которые определяют видимость разных объектов, составляющих сцену, вторичные лучи проводятся от точек пересечения к разным источникам света. При их блокировке объектом данная точка находится в тени, которую отбрасывает источник света. Для получения наиболее реалистичного рендеринга необходимо учитывать характеристики отражения и преломления материала, а для расчета финального цвета пиксела нужно проводить лучи отражения и преломления.

Рис. 6. Пример визуализации трассировки лучей

В визуализации у трассировки лучей много преимуществ: простота и элегантность, работа с отражениями и вторичными отражениями (рис. 6) (вывод отражений частей объекта друг на друге), возможность работы с искривленными поверхностями, качественная обработка эффектов прозрачности, расчет теней.

Однако есть и свои минусы. Одним из самых значимых недостатков трассировки лучей является медленность визуализации (рендеринга). Например, тот же рэй трейсер Mandelbulb 3D визуализирует изображение с большим количеством лучей и разрешением 4000 пикселов по длинной стороне около 30 мин, при увеличении детализации, а следовательно, и количества лучей рендеринг выполняется еще дольше. Если же оперировать значениями и таких параметров, как расчет жестких теней, расчет окружения, отражения и глубины поля зрения (FOV), то расчет итогового изображения увеличится пропорционально количеству лучей, и это несмотря на мощные и современные процессоры. Другой проблемой метода трассировки лучей является сглаживание. При трассировке лучи не учитывают реальные размеры. Прямым следствием такого эффекта будет появление «лесенок», что частично можно разрешить суперсэмплингом или рендерингом в большом разрешении, но опять же необходимо помнить о медленности рендеринга.

Рис. 7. Примеры изображений, синтезированных в программе Mandelbulber

Другим не менее мощным и прогрессивным инструментом для генерации трехмерных фракталов является программа Mandelbulber — экспериментальное приложение, разработанное для создания и работы с 3D­фракталами Мандельброта, а также с некоторыми другими видами 3D­фракталов, например Mandelbox, Bulbbox, Juliabulb, губка Менгера, Quaternion, тригонометрическими, гиперкомплексными и IFS, причем все формулы могут быть объединены в бесконечных вариациях. Особенности программы: великолепная гибкость в работе с 3D­фракталами, работа с освещением, тенями, цветом, поддержка эффектов ambient­окклюзии, глубины резкости и т.д. Неограниченное разрешение изображения на 64­битных системах. Простой в применении 3D­навигатор по фракталу. Программа поддерживает анимацию и абсолютно бесплатна. Mandelbulber, так же как и Mandelbulb 3D, использует трассировку лучей для отрисовки 3D­фракталов. Но вместо того, чтобы лучи проходили всю дистанцию между камерой и ближайшей поверхностью непрерывно, они проходят это расстояние дискретно. На каждом шагу моделируется рассеяние. Конечный результат представляет собой синтез различных состояний рассеяния вдоль всей длины луча.

Наряду с Mandelbulber и Mandelbulb 3D существует еще несколько программ, позволяющих визуализировать трехмерные фракталы, — Xenodream, Fragmentarium, Incendia, Chaoscope и др.

Хочется надеяться, что данная публикация оказалась для вас интересной, а главное — полезной. Ее целью было познакомить вас с основными и популярными сегодня программами­фракталогенераторами, а также с принципами их работы. Несмотря на ограниченное количество таких программ, возможности, которые они предлагают, практически неограниченны. Алгоритмы их работы и математический аппарат фракталов позволяют строить в этих программах самые фантастические фрактальные пейзажи, сцены и формы. И хотя большинство фракталогенераторов весьма просты в освоении, не стоит ждать, что, открыв впервые какую­нибудь программу, вы сразу сотворите в ней чудесный­расчудесный фрактал. Чтобы добиться хороших, красивых результатов в таком искусстве, как рисование фракталов, нужно терпение и много практики. Впрочем, как и везде. А посему всем удачи и творческого вдохновения в освоении программ и фрактального искусства в целом.

КомпьюАрт 1'2013