Применение свойств цифровых квадратов в процессах нерегулярного растрирования и дизайне

Э.В. Базазьян, канд. техн. наук1
С.П. Вартанян, канд. техн. наук, доцент кафедры ЕН, МГУП
Н.Э. Ядыкин, зав. лабораторией АПП, МГУП

Явление муара, проявляющееся в процессе многокрасочной печати полутоновых изображений при наложении регулярных растровых структур, хорошо известно полиграфистам, которые владеют методами, делающими этот паразитный эффект практически незаметным. Наиболее радикальным является применение нерегулярных растровых структур, наложение которых в принципе не приводит к образованию муара. Многие зарубежные фирмы предлагают полиграфистам свои разработки этого направления, причем технология применения подобных растровых структур довольно тщательно проработана [1]. Технологические исследования по созданию растров с нерегулярной структурой проводились и в нашей стране. Еще в 1970­х годах во ВНИИ полиграфии были созданы растры с нерегулярной структурой элементов для печатания высококачественных иллюстраций [2], однако дальнейшего развития эти разработки не получили.

Рис. 1

Новое направление в создании нерегулярных структур представляется возможным на базе свойств цифровых квадратов. Чтобы напомнить об этих свойствах, обратимся к одной истории.

В 1782 году российский математик швейцарского происхождения Леонард Эйлер сформулировал задачу о построении каре из 36 офицеров, представляющих шесть разных полков.

Предлагалось выстроить их таким образом, чтобы ни в одной шеренге и ни в одном ряду не было двух и более офицеров одного ранга и из одного полка. На основании своих исследований Л. Эйлер сделал предположение, что эта задача не имеет решения. Не найдено оно до сих пор.

Для заполнения квадратов Л. Эйлер первоначально использовал латинский алфавит (преподавание во всех средневековых университетах Европы велось на латыни). Так появилось название «латинский квадрат». Решая задачу о каре, ему пришлось использовать буквы и греческого алфавита. Для варианта 5x5 решение было найдено.

Если обозначить полки заглавными буквами греческого алфавита (A, B, G, D, E), а ранги офицеров строчными латинскими литерами (a, b, c, d, e), то получится каре в виде греко­латинского квадрата (рис. 1):

Третий представитель группы цифровых квадратов — магический квадрат еще до Эйлера использовался в оккультной сфере. Цифрам, которыми их заполняли, придавалось магическое значение, что и отразилось в названии таких объектов (эту тему в жанре детектива раскрывает американский писатель Дэн Браун [3] в увлекательном сюжете своего романа «Утраченный символ»).

Для латинского квадрата, в котором используется столько цифр, сколько клеточек в его строке (а также и в столбце), характерным является порядок цифр в каждом ряду или колонке, который не повторяется и дает особый результат — сумма цифр по строкам, столбцам и главным диагоналям для латинского квадрата одинакова. Например, для различных вариантов латинского квадрата 5x5 она равна числу 15.

Для греко­латинского квадрата характерна комбинация из двух цифр в каждой ячейке, причем как первые, так и вторые цифры каждой комбинации подчиняются правилам построения латинских квадратов.

Наконец, для магического квадрата, количество чисел в котором равно сумме его ячеек, правило размещения чисел в клеточках таково: как и в латинском квадрате, сумма чисел по строкам, столбцам и главным диагоналям одинакова. К примеру, для варианта 5x5 эта сумма равна числу 65 (рис. 2).

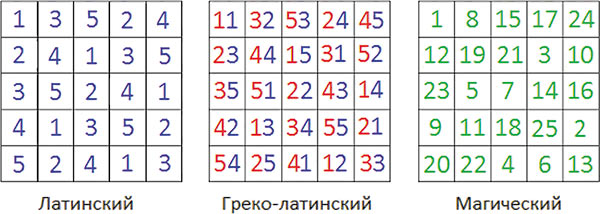
Рис. 2

В статье, опубликованной в университетском журнале «Вестник МГУП» № 8 за 2010 год [4], нами была рассмотрена возможность применения математического аппарата цифровых квадратов для создания нерегулярных растровых структур. В ходе обсуждения нашего предложения с коллегами2, проявившими интерес к данной работе, была выявлена необходимость более детального изложения некоторых аспектов приведенного в той публикации материала. В частности, вопросы касались возможного количества неповторяющихся размещений чисел в магических квадратах заданной размерности n, квазислучайности и равномерности распределения чисел ряда nxn в поле квадрата, наглядных примеров отсутствия паразитных структур в виде муара при взаимных наложениях растров, возможности многократного слияния мелких точек без потери стохастичности, примерных схем реализации предложенного способа. Все эти вопросы были рассмотрены во второй публикации «Вестника МГУП» [5], так что теоретические аспекты этого предложения изложены там более детально.

В результате был разработан математический аппарат, позволивший составить все рабочие формулы для получения и использования каждого из перечисленных типов цифровых квадратов различной размерности nxn (где n может иметь значения от единиц до десятков клеток по строке/столбцу квадрата).

Для выявления квазислучайности и равномерности распределения чисел ряда nxn в поле магического квадрата был проведен статистический анализ их размещения в выборке из 16 магических квадратов (МК).  Как известно [6], если некоторое событие при заданных условиях может произойти или не произойти, то оно называется случайным. Количественной оценкой возможности появления данного случайного события является его вероятность. Рассмотрим размещение чисел в ячейках поля магического квадрата с точки зрения теории вероятностей.

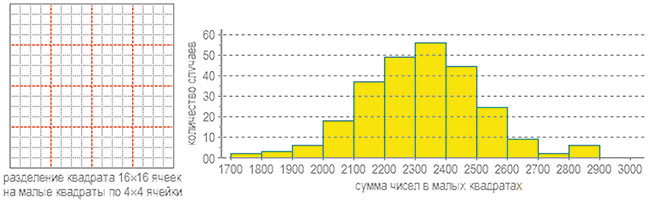
Рис. 3

В каждом из магических квадратов 16x16 размещается 256 чисел, и вероятность появления каждого из них в той или иной ячейке равна 1/256, если эти события случайны, а следовательно, равновероятны. То есть если взять несколько сот магических квадратов, то в каждой ячейке хотя бы раз появится каждое из 256 чисел. Такой эксперимент в обработке слишком трудоемок. Для упрощения математических выкладок разделим поле каждого из квадратов 16x16 на малые квадраты 4x4 и будем подсчитывать суммы чисел в каждом из них (рис. 3). Если числа по полю МК распределены равномерно, то значения сумм чисел в малых квадратах должны быть близки между собой, в чем можно убедиться на гораздо меньшем числе объектов, например, как в нашем случае, на 16 МК.  Для этих объектов были подсчитаны значения сумм чисел во всех малых квадратах (всего 256) и было рассчитано среднеарифметическое значение такой суммы:

а = Σ аi / n = 2348,25,

где:   аi — значение суммы чисел в i­м малом квадрате 4x4, n — общее число малых квадратов (256).

Для наглядности представления была построена гистограмма (см. рис. 3) распределения сумм по частоте встречаемости, которая явно указывает на нормальный закон распределения отклонений, характеризующийся Гауссовым распределением событий, дисперсией D и средним квадратическим отклонением σ:

где ε = аi – а есть отклонение суммы чисел в i­м малом квадрате 4x4 от среднего арифметического значения. Поскольку σ = 195,36 в процентном отношении к а = 2348,25 составляет около 8%, то большая часть значений сумм чисел малых квадратов лежит в данном допусковом пределе рядом со среднеарифметическим значением, а следовательно, числа от 1 до n² размещаются по полю магического квадрата случайно и равномерно.

Возможная схема реализации способа нерегулярного растрирования на основе применения магических квадратов в качестве образцов рандомизации (случайной выборки) представлена на рис. 4. Многие компоненты этой схемы присутствуют в современных системах сканирования полутоновых оригиналов, обработки полученной информации и вывода растрированного изображения на тот или иной носитель. Таким образом, реализация предлагаемого способа может вылиться аппаратно в отдельный чип (заказную микросхему) или даже чисто виртуально — в программный пакет.

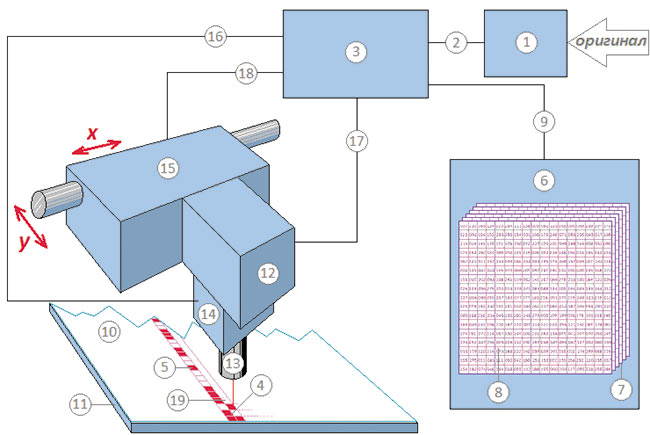
Рис. 4

Принцип действия схемы можно представить следующим образом. Устройство 1 (например, сканер) осуществляет преобразование оптических плотностей полутонового оригинала в электрические сигналы, которые там оцифровываются и передаются по каналу связи 2 в компьютерное устройство управления 3. В устройстве 3 производится преобразование значения оптической плотности каждого пиксела (элемента изображения) оригинала в соответствующий ей по относительной печатающей площади участок будущего растрового квадрата 4, выраженный в определенном количестве его предполагаемых рабочих ячеек 5. Какие именно ячейки данного растрового квадрата станут рабочими, определяется алгоритмом, заложенным в компьютерное устройство с учетом образца рандомизации, выданного источником 6, который является генератором массива 7 магических квадратов 8. Информация о координатах чисел в конкретном магическом квадрате передается от источника 6 в устройство 3 по каналу связи 9.

Все числа от 1 до m по одному заполняют ячейки магического квадрата. Общее количество всех ячеек принимается за 100%, и только k­я часть из них становится в растровом квадрате рабочей и заполняется печатными элементами, где k — количество ячеек из m, соответствующее требуемой относительной печатающей площади. Местоположение рабочих ячеек определяется в устройстве 3 порядком размещения чисел от 1 до k по взятому за образец магическому квадрату (рис. 5).

Рис. 5

Перед началом записи растровых квадратов на носитель информации 10 его закрепляют на рабочей поверхности 11 записывающего устройства (рекордера). Процесс записи осуществляется записывающей головкой 12 (например, лазерной), оснащенной объективом 13 и модулятором 14. Головка 12 перемещается по координатам х и у относительно носителя 10 с помощью механизма 15. Синхронизация команд на перемещение, запись и модуляция луча осуществляется устройством 3 через каналы связи 16, 17 и 18. От сигнала, поступающего по каналу 16 на модулятор 14 зависит, станет ли ячейка 19 записываемого растрового квадрата рабочей или останется пробельной. Поскольку массив 7 может содержать несколько миллионов «портретов» МК, то ими может без повторов быть заполнена площадь полутоновой иллюстрации формата А1 при линиатуре растра 60 л/см.

На данный способ был получен российский патент [7]. Если способ реализовать путем, программно совместимым с software действующих цифровых печатных машин, то, вероятно, его можно будет опробовать без существенных аппаратных разработок.

Рулонная цифровая печать позволяет создавать непрерывное полотно печатной продукции. Применение данного способа открывает новые возможности в дизайне — создавать массовую продукцию неповторимых рисунков. Простым примером тому может служить заставка к данной статье.

Если взять какую­либо палитру цветов (на рис. 6 использована штатная палитра рабочего кадра стандартной графической программы Paintbrush), то, присвоив каждому цвету десятичный цифровой код, можно отпечатать рулон в определенном стиле дизайна с неповторимым рисунком каждого метра этого полотна. Кратко методику можно изложить следующим образом.

Рис. 6

На рис. 6 палитра Paintbrush представлена парами цветов густого и светлого тона (бордовый — красный, зеленый — салатный, индиго — синий и т.п.). Также по порядку (слева направо и сверху вниз) расположены хроматические цвета и на верхнем левом квадрате 5x5, не являющемся стохастическим. В результате расположения цветов по алфавиту и присвоения им порядковых номеров (они приведены на рис. 6) был получен средний квадрат 5x5, который в определенной мере уже обладает стохастическими свойствами, поскольку инициалы названий цветов не подчиняются какой­либо математической формуле. Правый же квадрат заполнен цветами согласно порядку цифр в магическом квадрате, представленном на рис. 2. По этому образцу составлена левая половина изображения на заставке. Следующая порция изображения строится на «портрете» нового магического квадрата. По подобному принципу могут создаваться рисунки, скажем, упаковочной продукции, трикотажных изделий и других объектов, где при массовом производстве можно каждому экземпляру придать индивидуальные черты. 

Библиографический список

Кузнецов Ю.В. Основы подготовки иллюстраций к печати. Растрирование. Учебное пособие для вузов. М.: Изд­во МГУП «Мир книги», 1998. 174 с.

Андреева В.И. Оценка качества растрового изображения с нерегулярной структурой элементов / В.И. Андреева, А.Л. Попова // Труды ВНИИ полиграфии. Т.26. Вып. 1, 1977. С. 59­67.

Браун Дэн. Утраченный символ / Дэн Браун. М.: АСТ, 2010. 570 с.

Базазьян Э.В. Возможность применения математического аппарата цифровых квадратов в полиграфии / Э.В. Базазьян, С.П. Вартанян // Вестник МГУП. 2010. № 8.  С. 103­111.

Базазьян Э.В. Использование свойств цифровых квадратов в процессах нерегулярного растрирования / Э.В. Базазьян, С.П. Вартанян // Вестник МГУП. 2011. № 1. С. 23­29.

Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1984. 831 с.

Способ формирования растрового квадрата с нерегулярным заполнением ячеек печатными элементами. Российская Федерация. Патент на изобретение № 2466442 по заявке № 2011109491. Приоритет изобретения 14 марта 2011 г.

КомпьюАрт 11'2013