
Алгоритмы компрессии пиксельных изображений
I. Сжатие без потерь — простые алгоритмы
II. LZW-компрессия, и где она применяется
Статья посвящена существующим способам компрессии пиксельных изображений и ассоциированных с этими способами форматов файлов. Заинтересованный читатель найдет здесь краткое описание применяемых алгоритмов, понимание которых, по мнению автора, должно способствовать расширению кругозора (что уже хорошо), а также осмысленному выбору форматов хранения, обработки и пересылки файлов пиксельных изображений по компьютерным сетям.
Чтобы сэкономить время тех, кто не уверен, нужно ли ему читать эту статью, давайте сразу перечислим форматы файлов, о которых пойдет речь далее: TIF/LZW, GIF, PNG, PCD, JPEG, FIF(STN), WIF, DJVU.
Введение
Эпоха, в которую нам с вами довелось жить, ознаменована не только нестабильной политической ситуацией во многих регионах мира, не только скверным экономическим положением родной страны, но и, извините за банальность, бурными темпами развития компьютерной техники и технологий. Давайте вспомним хотя бы несколько вех, свидетелями которых мы с вами явились. Казалось бы, совсем не так давно были созданы первые персональные компьютеры и уже совсем недавно появились они у нас в стране. Мои ровесники-технари наверняка вспомнят первые ДВК, ЕС-1840 и пр., очередь на ночное время в класс персоналок, оснащенный PC/AT(!); фантастические оценки технического прогресса на то время, одна из которых гласила: «...если бы самолетостроение развивалось такими же темпами, как и производство микросхем, то сегодня мы могли бы несколько раз облететь земной шар без посадки и дозаправки». Теперь параметры тех машин кажутся нам смешными. Что такое 640 Кбайт оперативной памяти? Жесткий диск объемом 20 Мбайт?!
В работе над этой статьей я использую Power Mac 8100/80 cо 140 Мбайт «оперативки» и 6 Гбайт дискового пространства и завидую тому, кто имеет возможность жать на клавиши нового G3 (350 МГц!!!). И даже не важно, сколько там оперативной памяти и дискового пространства. Не за горами такие значения параметров компьютеров, как ГИГАБАЙТ оперативной памяти и несколько ТЕРАБАЙТ дискового пространства. И все это наряду с активным развитием разнообразных алгоритмов сжатия и упаковки информации, применяемых как аппаратно, так и программно... Так что же происходит вокруг: файлы становятся больше или больше становится файлов? Если разобраться, то имеет место и то и другое. Начнем с, казалось бы, простых текстовых файлов. Страница текста в «голом» виде занимает около 4 Кбайт, та же страница, сохраненная в несложном текстовом редакторе, занимает 13 Кбайт, и та же страница, сохраненная из MS Word, займет уже ~ 30 Кбайт. За удобство работы и новые возможности (включение в файлы информации об используемых шрифтовых гарнитурах, начертании, интерлиньяже, использование графики, звуков и даже видео) мы платим дисковым пространством и временем, необходимым для запуска пакета, умеющего обрабатывать все это богатство. Согласитесь, что отказывать себе в каких-либо возможностях, даже очень редко используемых, во имя сокращения времени доступа или размеров файлов мы уже не станем. Тем более что фирмы — производители «железа» и «софта» всячески потакают нашим неуемным аппетитам, предлагая все более совершенные устройства и программы. Что же говорить о графике, которая традиционно считалась весьма ресурсоемкой? Графические файлы по вполне объективным причинам тоже имеют тенденцию к «распуханию». За этой тенденцией прилежно следят производители программного обеспечения.
Весьма заметен прогресс в двух основных отраслях — потребителях графики: полиграфии (в широком смысле, включая широкоформатную малотиражную печать, изготовление bill-board’ов, сувенирной продукции и т.д.) и Web-дизайне. А применение новых технологий, диктуемое потребностями рынка, и влечет за собой «распухание» файлов. Если говорить о новых полиграфических технологиях, то среди них — печать больше чем в четыре краски (соответственно, нужно произвести цветоделение графического файла на 5, 6 или более виртуальных красочных слоев); печать с более высокой линиатурой растра (или с использованием стохастического растрирования), требующая большего разрешения пиксельных графических файлов. В области Web-дизайна требования к графике также повышаются — хотя бы в силу того, что мониторы, воспроизводящие 16,7 млн. цветов, уже не являются прерогативой профессионалов, а вполне доступны среднему компьютерному пользователю.
Что же происходит быстрее — рост наших потребностей в новых технологиях или технический прогресс? Ответ неоднозначен, поскольку появление неких технологий может спровоцировать спрос на товар или технологию, и наоборот — технология рождается в ответ на настоятельное требование рынка. Так или иначе, производительность новых, более совершенных поколений компьютеров вряд ли будет расти такими темпами, чтобы хотя бы на несколько лет вперед удовлетворить потребителей, благодаря чему технологии компрессии данных всегда будут востребованы и актуальны.
I. Сжатие без потерь — простые алгоритмы
Первым делом рассмотрим те алгоритмы, которые относятся к так называемым алгоритмам сжатия без потери качества (Lossless). Собственно, в основном они не имеют прямого отношения к графике, а работают с файлом как с набором данных.
Самым простым и в то же время достаточно эффективным является алгоритм RLE (Run Length Encoding), который применяется в большинстве архиваторов и сложных процедурах упаковки данных. Его суть очень проста. Если в структуре данных файла встречается фрагмент, состоящий из N-кратного повторения символа К, то этот фрагмент замещается выражением NK, например строка 116666726666384440000000, занимающая 24 байта (мы исходим из того, что для представления каждого символа используется слово из 8 бит или 1 байта), может быть представлена в виде: 21 46 7 2 46 3 8 34 70, занимающем уже всего 14 байт. Очевидно, что применение RLE будет более эффективно по отношению к файлам, имеющим в своей структуре большое количество повторяющихся фрагментов. Значит, перед тем как использовать RLE, надо определенным образом привести файл к такому виду. После рассмотрения этого примера у наблюдательного читателя может возникнуть вполне обоснованный вопрос: насколько оправданно (более правильно было бы сказать — оптимально) использование в данном примере целого байта для кодирования одного символа алфавита? Таким же вопросом задался американец Хуффман (Huffman), в 1952 году предложивший метод кодирования информации с помощью кодов переменной длины, который носит его имя даже несмотря на то, что с тех пор предложено большое количество усовершенствований этого метода и от него самого осталась лишь приблизительная схема. В основе этого метода лежит вероятностный подход к анализу появления символов используемого алфавита. Хорошо известно, что частота появления тех или иных символов, скажем русского алфавита, неодинакова. Буквы <Е> и <А> будут попадаться нам заведомо более часто, чем <З> или <Ъ>. Рассчитать вероятности появления тех или иных символов тоже не представляет трудности. Для этого надо просто подсчитать количество символов каждого вида в достаточно большом тексте (чем больше текст — тем точнее расчетная вероятность), после чего символам, имеющим более высокие вероятности появления, назначаются более короткие коды, а тем символам, которые редко встречаются, — более длинные.
Рассмотрим пример 1.
Пример 1
Пусть наш алфавит для простоты состоит из шести символов: <A>, <B>, <C>, <D>, <E> и <пробел> и известно, что вероятность появления символов в тексте сообщений такова:
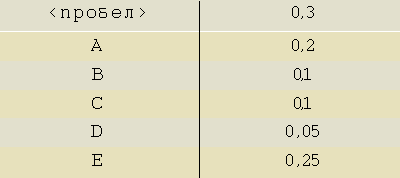
Если использовать стандартное двоичное кодирование символов нашего алфавита, то нам потребуется 3 бита на каждый символ:

Таким образом, для хранения 100-символьного слова потребуется 300 бит.
Сравним, какой выигрыш мы получим, если применим метод кодирования Хуффмана. Код может быть представлен в виде бинарного дерева, «листьями» которого являются символы нашего алфавита, а узлами — точки принятия решения о следующем символе кода.
Перейдем к составлению бинарного дерева кода Хуффмана переменной длины. Как мы уже знаем, оно составляется на основе данных о вероятностях появления символов. Следует отметить, что реальные алгоритмы, реализованные в программах сжатия, работают несколько иначе, что, однако, не меняет сути дела.
Начнем составлять дерево кода. Исходный список символов нашего алфавита с вероятностями их появления таков:
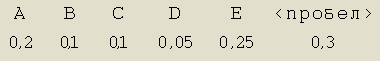
Шаг 1. Уберем из исходного списка два элемента, имеющие наименьшие вероятности появления. Возьмем С и D и сформируем новое ответвление, листьями которого станут вышеназванные символы, и просуммируем их вероятности.
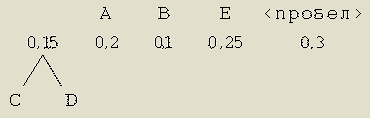
Шаг 2. Повторим процедуру из шага и сформируем новый ярус из элементов, имеющих наименьшие значения вероятностей.
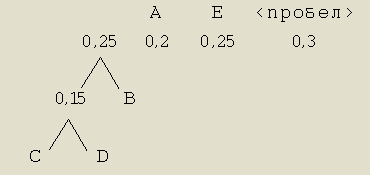
Шаг 3. То же, что и в предыдущих двух шагах. На этот раз формируем новое ответвление из элементов А и Е.
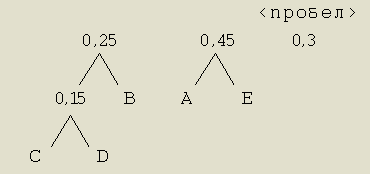
Шаг 4. Опять объединяем два элемента, имеющих наименьшие значения вероятностей.
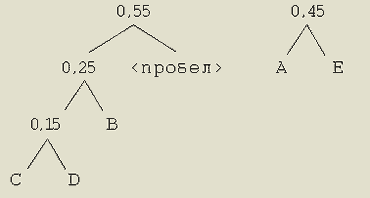
Шаг 5. Завершаем построение дерева.
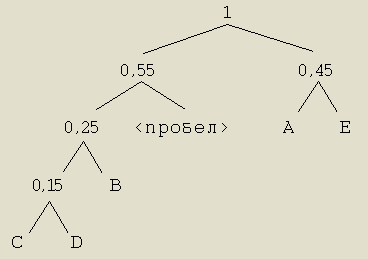
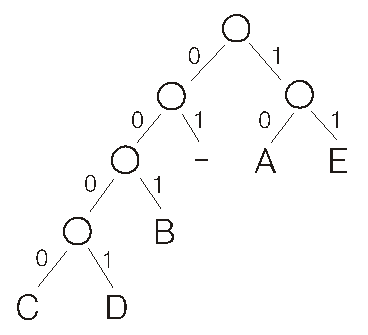

Количество бит, необходимое для хранения 100-символьного слова, рассчитаем по следующей формуле, учитывающей вероятность появления тех или иных символов:
100*0,2*A+100*0,1*B+100*0,1*C+100*0,05*D+ 100*0,25*E+100*0,3*<пробел>=
Подставим в формулу количества бит для каждого символа, полученные в результате Хуффмановского кодирования:
20*2+10*3+10*4+5*4+25*2+30*2=240
Для оценки эффективности работы алгоритма сжатия используется следующая формула:
(1–(объем сжатой информации/исходный объем информации))*100
Для нашего примера (1–(240/300))*100=20.
Иными словами, если мы применим алгоритм сжатия Хуффмана, то получим выигрыш в 20%. Что совсем неплохо для такого простого случая.
Теперь разберемся, что происходит с файлом на этапе раскодирования. Пусть мы получили по линии связи следующее двоичное слово:
10000000100010100011110
Может показаться, что процедура восстановления информации сложна из-за того, что применяется код переменной длины. Ведь вроде бы неизвестно, где кончается код предыдущего символа и начинается код следующего. Однако здесь все оказывается предельно просто.
Для раскодирования следует просто идти по нашему дереву кода, следуя последовательности символов входного потока, до тех пор пока не достигнем одного из листьев. Понятно, что следующий кодовый символ будет относиться уже к следующему коду.
Применим эту процедуру к приведенному выше двоичному слову, и получится (10) A (0000)C (001)B (0001)D (01)_ (0001) D (11)E (10)A. То есть исходная последовательность, закодированная с помощью кода переменной длины: ACBD_DEA.
Мы так подробно остановились на Хуффмановском кодировании, во-первых, потому, что оно очень часто применяется в алгоритмах компрессии данных, а во-вторых, потому, что следующий алгоритм, который применяется для компрессии графики, является развитием рассмотренного подхода, но с существенным усовершенствованием. Как было сказано, Хуффмановское кодирование базируется на знании вероятностей появления символов алфавита в тексте сообщения. Иными словами, его использование требует некоторой подготовительной работы или знания распределения вероятностей. А что делать, когда эти вероятности неизвестны и вычислить их не представляется возможным? Алгоритм, о котором пойдет речь ниже, не требует знания распределения вероятностей. Речь пойдет о LZW-компрессии, хорошо известной пользователям графических пакетов по опции при сохранении файлов в формате TIF (Tagged Image File Format — TIF/TIFF). Это, однако, не единственное применение этого алгоритма при компрессии графических файлов. Но давайте по порядку.
II. LZW-компрессия, и где она применяется
Основная идея, заложенная в алгоритмы компрессии данных, была предложена и реализована в начале 70-х израильтянами Якобом Зивом (Jacob Ziv) и Абрахамом Лемпелем (Abraham Lempel). Она заключается в замещении определенной фразы или группы байтов в наборе данных ссылкой на предыдущее появление этой фразы в том же наборе данных. Существует два основных класса схем, названных в честь своих изобретателей. Схемы были предложены, соответственно, в 1977 и 1978 годах — это LZ77 и LZ78.
Класс схем LZ77 нашел широкое применение при разработке различных программ-архиваторов, в том числе таких популярных, как ARJ и ZIP. Принцип работы этих схем заключается в том, что после заполнения данными определенного буфера происходит сравнение вновь поступившей строки данных с фрагментами, хранящимися в буфере, и если эта строка уже встречалась в каком-то месте буфера, то она замещается парой параметров (координата строки в буфере; длина строки). Этот класс схем еще иногда называют классом схем с «плавающим окном».
Но нас больше будет интересовать второй класс схем — LZ78, а точнее, самый известный представитель этого класса, которым является алгоритм LZW (Lempel-Ziv-Welch), разработанный в 1984 году Терри Уэлчем (Terry Welch) для применения в высокоскоростных контроллерах жестких дисков. Забегая вперед, скажу, что этот алгоритм используется в двух весьма распространенных графических форматах файлов, названных в начале этой статьи: GIF и TIF(LZW). Теперь кратко рассмотрим суть алгоритма LZW на примере 2.
Пример 2
Допустим, существует следующий набор данных в виде строки символов:/АБА/АВ/АВВ/АБВ
| Входная последовательность | Результирующий код | Значение ячейки словаря с соотв. строкой |
|---|---|---|
| /A | / | 256=/A |
| Б | А | 257=АБ |
| А | Б | 258=БА |
| / | А | 259=А/ |
| АВ | <256> | 260=/АВ |
| / | В | 261=В/ |
| АВВ | <260> | 262=/АВВ |
| / | <261> | 263=В/А |
| АБВ | <257> | 264=АБВ |
| <END> | В |
Рассмотрим, как работает алгоритм сжатия.
Исходная строка данных символ за символом поступает на вход условного кодирующего устройства. Результатом работы этого устройства является код, формирующийся на выходе.
Работа LZW-алгоритма начинается с формирования словаря объемом в 4 Кбайт, в которых с 0 по 255 хранятся отдельные символы, а с 256 по 4096 хранятся строки. Генерация каждого нового кода означает, что обработана еще одна строка. Новые строки формируются путем добавления текущего символа К к концу существующей строки W.
Алгоритм LZW-компрессии может быть описан так:
установить W = NIL (пусто)
цикл
считать символ K
если WK уже есть в словаре
W = WK
иначе
сгенерировать код для W
добавить WK в таблицу строк
W=K
конец цикла
Удивительная особенность этого алгоритма заключается в том, что для того чтобы распаковать сжатую информацию, нет необходимости передавать словарь. Он формируется автоматически аналогично алгоритму компрессии.
| Входная последовательность | Результирующий код | Значение ячейки словаря с соотв. строкой |
|---|---|---|
| / | / | |
| А | А | 256=/А |
| Б | Б | 257=АБ |
| А | А | 258=БА/ |
| <256> | /А | 259=А/ |
| В | В | 260=/АВ |
| <260> | /АВ | 261=В/ |
| <261> | B/ | 262=/АBB |
| <257> | AБ | 263=В/A |
| B | В | 264=АБВ |
Как уже говорилось, рассмотренный алгоритм LZW-компрессии применяется в двух распространенных форматах файлов графики: TIF(LZW) и GIF. В файлах формата TIF его применение будет тем эффективнее, чем больше в изображении, условно говоря, повторяющихся фрагментов,таких как однородный фон или области одного цвета. Соответственно, применение LZW-компрессии к файлам фотографических изображений или подобных им (с большим количеством полутонов, оттенков и деталей) дает весьма скромные результаты. Несмотря на то что в основе формата GIF лежит тот же, хотя и слегка видоизмененный алгоритм, этот формат заслуживает отдельного упоминания.
Формат GIF (Graphics Interchange Format) был разработан компанией UNISYS Corp и коммерческой телекоммуникационной сетью Compuserve специально, чтобы стимулировать обмен графическими файлами по телефонным линиям посредством модемов. Этот формат должен был объединить пользователей различных компьютерных платформ. Из-за того что скорость передачи данных через модемы сравнительно невысока, перед разработчиками этого формата стояла задача максимально возможного сокращения размеров графических файлов. Как мы знаем, эта задача была весьма успешно решена, в первую очередь за счет введения в формат определенных ограничений. GIF поддерживает только изображения с глубиной цвета 8 бит, то есть может содержать информацию лишь о 256 цветах. Во времена, когда цветные компьютерные мониторы в основной своей массе были в состоянии отобразить только эти самые 256 цветов, а приборы, предназначенные для воспроизведения 16,7 млн. цветов (так называемый TrueColor), были еще сравнительной редкостью, подобное ограничение не казалось чрезмерным. Но возникает законный вопрос: как отобрать эти 256 цветов, в каком виде их хранить и каким образом корректно отображать? Эта проблема была решена разработчиками формата c помощью применения серий таблиц цветовых ссылок или так называемый CLUTs (Color Look Up Tables). Они хранят проиндексированные цвета, которые содержатся в изображении. Отсюда и пошло название цветовой модели Indexed Color. Из всего предыдущего описания становится ясно, что эффективность применения формата GIF обусловлена введением ряда ограничений на хранимое в этом формате изображение. Как мы уже знаем, используемый алгоритм компрессии (LZW) тем эффективнее, чем меньше в изображении оттенков цветов и мелких деталей. Таким образом, в этом формате оптимально сохранять простые изображения, такие, например, как карикатуры и штриховые изображения. Если же сохранять в GIF фотоизображения, то уровень компрессии будет меньше, а кроме того, значительная часть цветовой информации будет безвозвратно утеряна, что может недопустимо исказить изображение. Тем не менее в течение определенного времени формат GIF был бесспорным лидером в области передачи графики по компьютерным сетям. До сих пор можно сказать, что его применение эффективно для класса изображений, условно называемых простыми.
Ограничения, названные ранее, стимулировали развитие новых форматов хранения (компрессии) изображений. В развитие GIF, а также с целью вытеснения его с рынка независимая группа разработчиков PNG Development Group разработала формат PNG (Portable Network Graphics), использующий уже известный нам механизм компрессии LZ77 (см. выше) с Хуффмановским кодированием переменной длины. Этот формат обладает рядом существенных преимуществ перед своим предшественником и конкурентом. Прежде всего все разработчики программного обеспечения могут совершенно свободно создавать пакеты для редактирования и сохранения изображений в этом формате, в то время как владельцем соответствующих прав на формат GIF являлась сеть Compuserve (теперь — America Online). Сняты ограничения на используемую цветовую модель. PNG поддерживает глубину цвета до 16 бит и дополнительные альфа-каналы. В файле может храниться информация о цвете и об используемой гамме, что очень важно при применении систем управления цветом. Кроме того, PNG хорошо приспособлен для использования в World Wide Web, поскольку он достаточно просто обрабатывается программами коррекции ошибок. В общем, PNG — вполне современный и удобный формат, уступающий GIF только в том, что не поддерживает анимацию. Однако «раскручивать» его некому, да и средств это требует немалых, поэтому, на мой взгляд, надежда разработчиков на то, что пользователи и разработчики программ откажутся от GIF и перейдут на «халявный» PNG, не вполне оправдалась. Впрочем, стоит отметить, что наличие этого формата в списке поддерживаемых форматов пакета Adobe Photoshop — бесспорного лидера в отрасли — уже говорит об определенном признании заслуг разработчиков.
До сих пор мы рассматривали форматы, использующие алгоритмы компрессии без потерь качества (lossless). К этому классу относятся те алгоритмы, которые позволяют после компрессирования файла открыть его с теми же линейными размерами и с тем же разрешением без искажений. Однако со временем было замечено, что человеческое зрение устроено таким образом, что позволяет в ряде случаев снижать требования к характеристикам файлов без видимого искажения изображения, хотя, строго говоря, в этом случае необходимо говорить об определенных потерях. Алгоритмы, относящиеся к этому классу (так называемые lossy), получили широкое распространение в силу сочетания высокого уровня компрессии и визуального отсутствия потери качества изображения после осуществления компрессии.
Начнем рассмотрение названного класса lossy с формата PCD (Kodak PhotoCD). Этот формат, имеющий ряд интересных особенностей, не получил широкого распространения (по сравнению с GIF и JPEG) в силу политики фирмы Kodak, накрепко привязавшей возможность сохранения в PCD к аппаратно-программному комплексу, предназначенному для производства CD с изображениями, записанными по фирменной технологии. Этот комплекс может быть представлен различными конфигурациями в зависимости от пожеланий заказчика и его бюджета, но в общем случае он включает в себя сканер, рабочую станцию (Sun SparcStation), CD-recorder и принтер, а также необходимое программное обеспечение. Стоимость подобного набора для производства Kodak PhotoCD составляет от нескольких тысяч до нескольких десятков тысяч долларов США. Отсюда видно, что не каждый компьютерный художник или фотоателье купит себе подобную «игрушку». Технология же, лежащая в основе формата Kodak PhotoCD, весьма оригинальна. Начнем с того, что для этого формата было разработано специальное цветовое пространство, получившее название Photo YCC.
Достаточно развернутое рассмотрение этого пространства, которое последует далее, — отнюдь не отступление от темы данной статьи, как может показаться на первый взгляд. Дело в том, что механизмы компрессии изображений, задействованные в этом формате, частично используют особенности кодировки цветовой информации.
Дальний родственник и предшественник Photo YCC — цветовое пространство YIQ, разработанное в начале 50-х годов для нужд только нарождавшегося цветного телевизионного вещания. Проблема, вставшая тогда перед вещательными компаниями, состояла в нахождении способа такой кодировки телевизионного изображения, которая бы подходила как для черно-белых телевизионных приемников, так и для появлявшихся цветных. YIQ представляет собой трехкоординатное цветовое пространство, в котором координата Y отражает уровень яркости, то есть монохромный канал, собственно принимаемый и отображаемый черно-белым телевизором, а две координаты I и Q характеризуют цвет в данной точке. Пространство Photo YCC построено на том же принципе, но имеет гораздо больший цветовой охват, включающий даже те цвета, которые находятся за порогом человеческого восприятия. Сделано это в расчете на самые совершенные современные технологии цветопередачи и цветовоспроизведения, а также на еще более совершенные технологии, которые появятся в будущем. Большим достоинством пространства Photo YCC является простота его пересчета в другие цветовые пространства, которые могут понадобиться пользователю формата PCD, такие как RGB и CIELab. Поскольку исходным цветовым пространством, в котором работают сканеры, является RGB (правда, RGB конкретного сканера), приведем пример формул пересчета координат из RGB в Photo YCC.
Сначала производится гамма-коррекция:
Для R,G,B > 0.018 R’ = 1.099*R0.45 — 0.099 G’ = 1.099*G0.45 — 0.099 B’ = 1.099*B0.45 — 0.099
Для R,G,B < –0.018 R’ = –1.099*R0.45 + 0.099 G’ = –1.099*G0.45 + 0.099 B’ = –1.099*B0.45 + 0.099
Для –0.018 < R,G,B < 0.018 R’ = 4.5*R G’ = 4.5*G B’ = 4.5*B
Любопытно, что значения RGB после гамма-коррекции (R’G’B’) будут верны до тех пор, пока вы не сделаете какой-нибудь глупости, например, не откалибруете свой монитор ради линеаризации его излучений.
Затем значения R’G’B’ пересчитываются в координаты Photo YCC (Luma, Chroma1, Chroma2) по следующим формулам:
Luma= 0.299R’ + 0.587G’ + 0.114B’ Chroma1 = -0.299R’ — 0.587G’ + 0.886B’ Chroma2 = 0.701R’ — 0.587G’ — 0.114B’
В завершение дробные значения координат должны быть преобразованы к виду целых восьмиразрядных чисел (от 0 до 255) для сохранения в файл.
Luma8bit= (255 / 1.402)Luma Chroma18bit= 111.40*Chroma1 + 156 Chroma28bit= 135.64*Chroma2 + 137
Несимметричность (взаимный относительный сдвиг) цветовых координат Chroma1 и Chroma2 отражает, по мнению Kodak, существующее распределение цветов в реальном мире. Эта несимметричность лучше всего видна на примере кодировки нейтрального серого цвета. Например, 20%-ный серый в пространстве Photo YCC будет иметь координаты:
Luma8bit = 79 Chroma18bit = 156 Chroma28bit = 137
Обратный пересчет из Photo YCC в RGB, например для отображения на компьютерном мониторе, не является инверсией приведенных выше расчетов, а представляет собой иную последовательность действий.
Сначала мы должны восстановить дробные значения координат в пространстве Photo YCC.
Luma = 1.3584 * Luma8bit Chroma1 = 2.2179 * (Chroma18bit — 156) Chroma2 = 1.8215 * (Chroma28bit — 137)
Затем (для мониторов, чьи характеристики близки к CCIR 7091) рассчитываем значения RGB по следующим формулам:
R’ = Luma+ Chroma2 G’ =Luma — 0.194Chroma1 — 0.509Chroma2 B’ = Luma + Chroma1
Обратите внимание на две вещи: во-первых, согласно приведенным формулам, значения RGB изменяются в пределах от 0 до 346 (вместо привычного диапазона от 0 до 255), что говорит о большем цветовом охвате Photo YCC, причем основная часть цветовой информации, которая будет потеряна при прямом пересчете в иное цветовое пространство с меньшим цветовым охватом, будет находиться в области «светов». Поэтому для получения 8-битных координат используются нелинейные функции, например:
Y = (255/1.402)*Y’ C1 = 111.40*C1'+156 C2 = 135.64*C2'+137;
во-вторых, если характеристики монитора, который предполагается использовать, значительно отличаются от приведенных в CCIR 709, для пересчета координат Photo YCC в пространство этого монитора потребуется использовать промежуточное аппаратно-независимое пространство, например CIE XYZ.
Теперь рассмотрим, в каком виде на дисках PhotoCD хранятся файлы изображений, представленных в описанном выше пространстве Photo YCC.
Напомним, что особенностью файлов формата PhotoCD является возможность открыть их в одном из шести вариантов разрешения.
Перед тем как файл будет записан на PhotoCD, программа, называющаяся Kodak PCD Data Manager, разбивает изображение на систему компонентов, каждый из которых представляет собой файл изображения в одном из вариантов разрешения. Основным вариантом, называемым Base, выбран вариант разрешения 512 линий на 768 пикселов. Названия остальных компонентов отражают их соотношение с основным. Они приведены в таблице вместе с рекомендованным фирмой Kodak назначением.
Первые пять компонентов хранятся в одном файле, называемом ImagePAC, при этом первые три хранятся в несжатом виде. Шестой компонент хранится в виде отдельного файла, называемого ImagePAC Extension (IPE), и записывается в качестве дополнения только на дисках PhotoCD Pro Master.
Если теперь мы посчитаем, сколько места должны занимать первые 5 файлов в таблице без использования каких-либо методов компрессии, мы получим в сумме около 24 Мбайт, в то время как типичный размер ImagePAC составляет около 5 Мбайт. Таким образом, налицо компрессия данных больше чем в 4 раза! За счет чего же достигается такой показатель? В этом формате применено два приема:
1. В два раза (в вертикальном и горизонтальном направлении) снижено разрешение красочных каналов Chroma1 и Chroma2. В результате на каждый пиксел красочных каналов приходится по 4 пиксела канала Luma. Этот прием использует особенность человеческого восприятия изображения, когда вариации в тоне не так важны, как вариации в яркости, а также особенности цветового пространства Photo YCC. Обработанное таким образом изображение практически неотличимо на глаз от оригинала (если за оригинал считать файл, в котором у красочных каналов сохранено исходное разрешение). Один только этот прием позволяет уменьшить файл сразу в два раза.
2. Существенное уменьшение объема файла достигается путем декомпозиции файла высокого разрешения и сохранения 4Base, 16Base и 64Base как разности между этим файлом и файлом предыдущей ступени разрешения. Помимо этого к файлу применяется уже знакомая нам процедура Хуффмановского кодирования (см. выше). Принятая схема позволяет довольно легко «рассчитать» изображение нужного разрешения прямо в буфере монитора.
Поясним, каким образом «рассчитываются» изображения необходимого разрешения. Для получения изображения 4Base (1024 * 1536) берется предыдущее изображение — Base (512 * 768) (как мы помним, оно хранится без компрессии) и интерполируется до искомого размера (1024 * 1536), затем к файлу разности 4Base применяется процедура Хуффмановского декодирования, и полученные данные добавляются в соответствующие пикселы интерполированного изображения. В результате получается полноценное изображение с разрешением 1024 * 1536. Аналогично для получения полноценного изображения следующей ступени разрешения (2048 * 3072) берется компонент Base, с ней проводятся все ранее описанные процедуры, после чего изображение опять интерполируется до искомого разрешения и к нему добавляется декодированная информация уже из разности 16Base и т.д. Как видно из приведенного описания, формат PCD обладает рядом особенностей, в силу которых его применение весьма ограничено — в основном он используется для сохранения библиотек фотоизображений. Более широкого распространения в существующем виде он по уже названным причинам не получит.
Следующим представителем класса lossy и, пожалуй, самым известным и распространенным в наше время является формат JPEG. Строго говоря, JPEG — это не формат файла, как например TIFF или JFIF (JPEG Interchange File Format — корректное название обсуждаемого формата файла), а метод компрессии графических изображений, получивший свое имя в честь коллектива Joint Photographic Experts Group, специально созданного для разработки методов компрессии фотоизображений, — иными словами, для изображений, в которых присутствует большое количество цветов, полутонов и оттенков. В переводе на русский язык название этой группы звучит как Совместная группа экспертов по фотографии. Совместная потому, что была создана при содействии двух международных организаций: ISO2 и CCITT (см. примечание 1). Разработанный группой метод, получивший название JPEG-компрессии, позволяет сжимать фотоизображения в десятки раз при сравнительно небольшом снижении качества (достаточно типичным уровнем компрессии является 30:1). При этом пользователь может выбрать необходимое ему соотношение качества (точнее, потери качества) и размера файла. Метод JPEG-компрессии основан на том же принципе, который рассматривался при описании формата PCD, — особенности человеческого восприятия изображений.
Человеческий глаз более четко различает абсолютную яркость объектов, цветовые области и их границы, нежели небольшие изменения в тенях и мелкие детали. Таким образом, при сохранении файла изображения часть цветовой информации может быть просто отброшена без ущерба для восприятия. Делается это уже известным нам путем, использованным в формате PCD. Изображение переводится в цветовое пространство YCbCr 3, а затем разрешение двух цветовых каналов (CbCr) уменьшается. Этим способом можно уменьшить размер итогового файла в 2-4 раза (в зависимости от степени снижения разрешения красочных каналов). Затем изображение разбивается на фрагменты размером 8*8 пикселов, и над этими матрицами производятся достаточно сложные математические преобразования, называющиеся дискретными косинусными преобразованиями (discrete cosine transforms (DCT)4) и квантованием. Изменения цвета и яркости в каждой матрице до определенной степени округляются. Причем степень округления увеличивается сообразно округляемому числу, делая, таким образом, небольшие изменения более весомыми. Например, различие в 3 единицы может быть округлено до 5, а значение 75 может быть округлено до 100. Результатом преобразования каждой исходной матрицы является матрица, которая также описывает исходное изображение, правда, уже не так точно. Ее особенностью является то, что она состоит по большей части из коэффициентов, имеющих одинаковые значения (точнее говоря — нулей) и поддающихся очень эффективному сжатию с помощью рассмотренных ранее способов компрессии «без потерь», например, путем применения Хуффмановского кодирования и RLE (см. выше). По сравнению с рассмотренными ранее формат JPEG имеет ряд особенностей, позволяющих говорить о том, что его использование оптимально в отношении полутоновых цветных изображений, таких как отсканированные цветные фотографии.
Весьма любопытными алгоритмами компрессии, которые также относятся к классу lossy, являются алгоритмы FIF (STN), основанные на так называемой фрактальной геометрии (fractal geometry), в свою очередь, базирующейся на теории приближений, впервые упомянутой в 1918 году в работе французского математика Гастона Мориса Джулиа (Gaston Maurice Julia), озаглавленной Memoire Sur L’iteration Fonctions Rationalles. Гастон Морис изучал так называемые наборы Джулиа (Julia sets) — математические объекты, состоящие из итераций полиномиальных функций, и сформулировал идею, согласно которой весь набор может быть воссоздан по сравнительно небольшому фрагменту. Ученик Гастона Мориса математик Бенуа Мандельброт (Benoit. B. Mandelbrot), работая в корпорации IBM, вернулся к теме, изучавшейся его учителем, но в несколько ином приложении. Он поставил под сомнение возможность использования традиционной (евклидовой) геометрии для описания таких объектов окружающего нас мира, как пейзажи и деревья. В качестве примера в своих ранних исследованиях Мандельброт рассматривал карту побережья Великобритании. Давайте вслед за Мандельбротом посмотрим на карту (см. приложение 2). По ней с определенной степенью точности можно измерить длину береговой линии. Однако если мы приблизимся к рассматриваемому объекту (возьмем карту существенно более мелкого масштаба), то увидим внутри уже известных нам заливов множество более мелких заливов и полуостровов. Здесь мы можем с определенной точностью вновь измерить длину береговой линии. Нет нужды говорить, что она окажется существенно больше той, что была получена нами на предыдущем этапе. Теперь представим себе, сколько подобных итераций мы можем произвести. Вообще говоря, сколько угодно, то есть бесконечное множество, причем длина измеренной нами береговой линии будет также стремиться к бесконечности. Для описания именно таких объектов Мандельброт предложил использовать фрактальную геометрию. В 1977 году Мандельброт опубликовал книгу «Фрактальная геометрия природы», основной мыслью которой является то, что традиционная геометрия с ровными поверхностями и прямыми линиями не может быть применена для описания таких объектов, как облака, скалы и пейзажи, а фрактальная геометрия с ее бесконечной детализацией и замысловатыми контурами идеально для этого подходит. «Фрактальная геометрия играет сразу две роли. Это геометрия детерминистского хаоса и вместе с тем это геометрия гор, облаков и галактик», — писал Бенуа Мандельброт. Термин фрактал (fractal), введенный Мандельбротом в 1975 году для обозначения примитива, используемого для построения изображений, которыми оперирует фрактальная геометрия, происходит от латинского слова fractus, обозначающего нерегулярную поверхность, такую, например, как поверхность расколотого камня. Фракталы — нерегулярные геометрические формы, имеющие одинаковую степень нерегулярности во всех измерениях. Как камень, лежащий у подножия скалы, напоминает всю скалу в миниатюре, фрактал напоминает все изображение, созданное с его помощью. Поскольку фракталы есть не что иное, как математические объекты, Мандельбротом был изобретен математический способ генерации пейзажей. Если возможно рассчитать большое изображение по фрагменту, то почему бы не использовать этот механизм для компрессии? Программы компрессии, использующие описанный подход, «просматривают» изображение на предмет выявления фрагментов, которые могут быть получены друг из друга применением так называемых аффинных преобразований5. Такие фрагменты встречаются в любом изображении. Далее вместо фрагмента записывается ссылка на исходный фрагмент и последовательность его преобразований в виде математических формул. При этом получаемые фрагменты не идентичны исходным, а аффинны. Из этого следует, что этот механизм компрессии в определенной степени ухудшает качество сжатого изображения, то есть является lossy. В зависимости от вида изображения вносимые искажения могут быть малозаметными или значительными. Так, фотоизображения страдают гораздо меньше, чем графики и чертежи. Уровень компрессии, достижимый при применении названных алгоритмов, теоретически может достигать 1000:1, однако на практике он не превышает 50:1. Как и другие способы компрессии, этот способ имеет свои достоинства и недостатки. К достоинствам следует отнести сравнительно высокий уровень компрессии, возможность работать с файлами, представленными в любой цветовой модели (кроме Lab), и большую скорость распаковки файла. Существенным преимуществом фрактальной компрессии, вытекающим из природы формата (то есть того факта, что файл сжатого изображения представляет собой несколько фракталов и список математических действий, которые необходимо над ними произвести для восстановления полного изображения), является возможность открыть сжатый файл теоретически с любым разрешением. Этим свойством формата особенно козыряет производитель программ Genuine Fractals и PrintPro — Altamira Group, утверждая, что одно и то же изображение, должным образом подготовленное и сохраненное в формат FIF (STN)6, может быть использовано как для журнальной печати (допустим, в качестве полосной иллюстрации), так и для печати плакатов. При этом не будет заметно снижение качества. Действительно, при задании более высокого разрешения при распаковке (что позволяют делать названные выше программы) не наблюдается увеличения числа пикселов исходного изображения, что неизбежно происходит, если мы пытаемся увеличить разрешение пиксельного файла «в лоб» в Photoshop. Изображение лишь теряет резкость. Действительно, в ряде случаев этим эффектом можно пренебречь, особенно если конечная продукция предусматривает просмотр с некоего расстояния, допустим с одного-трех метров. Однако извечная мечта компьютерных художников — иметь возможность масштабировать пиксельные изображения так же свободно, как и векторные, пока остается только мечтой.
К недостаткам фрактальной компрессии следует прежде всего отнести значительное время, требующееся на компрессию (сохранение) изображения. Кроме того, этот формат не получил пока что значительного распространения и поэтому не поддерживается никакими другими популярными программами.
Еще одним форматом класса lossy, менее распространенным, но достойным упоминания по причине, которая будет названа ниже, является формат WIF. WIF — Wavelet Image Format 7 появился благодаря изобретенному в Хьюстонском центре передовых исследований (Houston Advanced Research Center — HARC) математическому методу компрессии данных, названному «волновым преобразованием» (Wavelet Transform). Результатом применения волнового преобразования изображения является математическое выражение, значительно меньшее по объему занимаемой памяти, чем оригинал. Достижимые уровни компрессии, по словам авторов изобретения, составляют сотни раз (до 300:1) при сравнительно высоком качестве изображения, что превышает характеристики JPEG-компрессии. Кроме того, благодаря применению волнового преобразования при высоких уровнях компрессии удается избежать появления явно выраженной «мозаичной» структуры изображения, характерной для JPEG-компрессии. Не вдаваясь в детали, все же скажу, что собранная мною из разных источников информация о внутреннем устройстве формата говорит о том, что алгоритм, использованный в этом формате, представляет собой некую суперпозицию уже описанных выше алгоритмов, использованных в форматах JPEG (с заменой DCT на волновое преобразование) и PCD. Формат этот, как известно, не является распространенным. К сожалению, мне не удалось найти ни одной программы для Macintosh, которая бы «умела» сохранять пиксельные изображения в этот формат, поэтому удостовериться в справедливости утверждений авторов изобретения мне не удалось. Мое внимание к WIF привлек тот факт, что в работе над новой версией формата JPEG (JPEG 2000), ставшего de facto отраслевым стандартом, принимает участие немецкая компания LuraTech, активно продвигающая на рынок программы, использующие алгоритм волнового преобразования. Заявленные свойства нового формата JPEG 2000 — отсутствие искажения исходного изображения и более высокие уровни компрессии — по мнению разработчиков, достижимы при использовании алгоритма волнового преобразования. Авторитет разработчиков формата JPEG неоспорим. И то, что из множества перспективных разработок по компрессии было выбрано именно волновое преобразование, свидетельствует в пользу того, что мы с вами еще не раз услышим это название, а может быть, даже будем им пользоваться.
В заключение нашего обзора алгоритмов компрессии пиксельных изображений рассмотрим еще один формат — DjVu, предназначенный для решения конкретной прикладной задачи — оцифровки печатной продукции (книг, каталогов, брошюр, газет, исторических документов и т.п.). Книги, как и другие печатные изделия, в отличие от цифровых данных, подвержены старению, а потому рано или поздно все библиотеки мира вынуждены будут задуматься над сохранением для потомков накопленного богатства. Причем речь идет о таком виде хранения, который предусматривал бы возможность получения доступа к хранимым материалам всех заинтересованных лиц. То есть решение проблемы путем помещения оригинала в стеклянный резервуар, наполненный инертным газом, и хранение его при полном отсутствии освещения явно не имеет смысла. С бурным развитием Интернета стал возможен удаленный доступ пользователей Всемирной сети ко множеству самых разнообразных видов ресурсов, одним из которых, естественно, должны стать библиотеки. Простое сканирование книжных страниц не дает искомого результата. Если мы ставим перед собой цель сделать текст читабельным после сканирования, то файл изображения должен быть достаточно большим. В этом случае нужно забыть об удаленном «листании» книжек, даже при использовании самых высокоскоростных устройств доступа к сети. Если же мы сожмем (используя стандартные форматы вроде JPEG или GIF) файлы до размера, который позволит быстро загружать изображения в окно браузера, то текст, особенно мелкий, может превратиться в невнятное пятно, не поддающееся расшифровке. Свое решение названной проблемы предложили инженеры одного из подразделений американской компании AT&T — одного из лидеров на рынке телекоммуникаций. AT&T Labs-Research — новое название части Bells Laboratories — колыбели науки о методах компрессии. Предложенная ими технология, получившая название DjVu [«дежавю» —deh zha vu], что в переводе с французского означает: «уже виденное», базируется на следующей идее. Любая печатная страница представляет собой композицию из всего двух принципиально отличающихся типов объектов: изображений (картинок) и шрифтовых символов. Изображения характеризуются отсутствием резких контуров и большим количеством полутонов, а шрифтовые символы — наличием четких очертаний и ровного цветового заполнения. Эти два типа объектов разделяются, а затем сжимаются с использованием разных методов компрессии. Полутоновые изображения обрабатываются с помощью алгоритма IW44, базирующегося на волновом преобразовании (см. выше), а текст и штриховые изображения — с помощью алгоритма JB2, специально предназначенного для эффективного сжатия штриховых изображений. Достигаемая при использовании DjVu удобочитаемость страниц при полном сохранении впечатления от иллюстраций просто восхищает. А размеры файлов позволяют скачивать их за секунды. Типичная четырехкрасочная журнальная страница при разрешении 300 dpi, будучи сохранена в DjVu, займет всего от 40 до 70 Кбайт (!!!). Обратите внимание, что и в этом формате используются так называемые волновые преобразования (Wavelet Transforms). На сегодня ассортимент программ, предлагаемых AT&T для работы с DjVu, невелик. Он включает plug-in для браузера (Netscape или Explorer), программу компрессии (как обычно, для Macintosh ее еще не существует, хотя планируется выпустить в ближайшем будущем) и SDK (Software Development toolKit) — пакет для программирования, то есть встраивания в вашу программу возможности сохранения в DjVu. При всех любопытных особенностях формата DjVu область его применения весьма ограниченна. Но вполне вероятно, что технологические решения, обкатываемые разработчиками на DjVu, послужат в дальнейшем для разработки более совершенного и универсального формата.
Подводя итог сказанному, хочется отметить, что общая тенденция к унификации используемых форматов, наряду с повышением требований к качеству изображений и размеру соответствующих файлов, продолжает стимулировать появление новых разработок в этой области. Но дальновидные ученые пытаются не только найти оптимальные пути решения сегодняшних задач, но и заглянуть в будущее, чтобы представить себе, какими будут задачи следующего века, следующего тысячелетия, тем более что до его начала осталось менее года. Ну а нам, пользователям, необходимо самым тщательным образом следить за новинками, обучаясь по мере продвижения прогресса в нашей области, в чем и желаю всем больших успехов.
Петр Нуждин, зам. генерального директора ООО «Дизайн-Центр Коммерсант» pet@kommersant.ru
КомпьюАрт 2'2000